
Mundarija:
- Muallif John Day day@howwhatproduce.com.
- Public 2024-01-30 13:30.
- Oxirgi o'zgartirilgan 2025-01-23 15:14.
Kirish
Ushbu qo'llanma elektronika loyihalarida akselerometr va giroskoplarni, shuningdek, IMU kombinatsiyali qurilmalarini (inertial o'lchov birligi) ishlatishni istagan har bir kishiga mo'ljallangan.
Biz qamrab olamiz:
- Akselerometr nimani o'lchaydi?
- Gyroskop (aka giro) nimani o'lchaydi?
- Sensordan olingan analog-raqamli (ADC) o'qishni jismoniy birliklarga qanday o'zgartirish mumkin (akselerometr uchun g, giroskop uchun deg/s).
- Qurilmangizning er tekisligiga nisbatan moyilligi haqida aniq ma'lumot olish uchun akselerometr va giroskop o'qilishini qanday birlashtirish mumkin
Maqola davomida men matematikani minimal darajaga tushirishga harakat qilaman. Agar siz Sine/Cosine/Tangent nima ekanligini bilsangiz, siz qaysi platformadan foydalanmasligingizdan qat'i nazar, loyihada bu g'oyalarni tushunishingiz va ishlatishingiz kerak: Arduino, Propeller, Basic Stamp, Atmel chipslari, Microchip PIC va boshqalar.
U erda odamlar borki, sizga IMU birligidan foydalanish uchun murakkab matematika kerak (Kalman filtrlari, Park-McClellan filtrlari va boshqalar kabi murakkab FIR yoki IIR filtrlari). Siz bularning barchasini o'rganishingiz va ajoyib, ammo murakkab natijalarga erishishingiz mumkin. Mening narsalarni tushuntirish usuli oddiy matematikani talab qiladi. Men soddaligiga ishonaman. O'ylaymanki, oddiy tizimni boshqarish va kuzatish osonroq, bundan tashqari, ko'pgina o'rnatilgan qurilmalarda matritsa hisobini talab qiladigan murakkab algoritmlarni amalga oshirish uchun kuch va resurslar yo'q.
Men misol sifatida yangi IMU birligini, Acc_Gyro Accelerometer + Gyro IMU ni ishlataman. Quyidagi misollarda biz ushbu qurilmaning parametrlaridan foydalanamiz. Bu qurilma boshlash uchun yaxshi qurilma, chunki u 2 ta qurilmadan iborat:
- LIS331AL (ma'lumotlar varaqasi) - uch fazali 2G akselerometr - LPR550AL (ma'lumotlar varaqasi) - ikki o'qli pitch va roll, 500 gradus/sekundli giroskop
Ular birgalikda 5 graduslik erkinlik inertial o'lchov birligini ifodalaydi. Endi bu ajoyib ism! Shunga qaramay, chiroyli ismning orqasida biz juda foydali kombinatsiyali qurilma bor, biz bu qo'llanmada batafsil yoritib beramiz.
1 -qadam: akselerometr
Bu birlikni tushunish uchun biz akselerometrdan boshlaymiz. Akselerometrlar haqida o'ylayotganda, ko'pincha kub shaklidagi qutini, ichida to'p borligini tasvirlash foydali bo'ladi. Siz cookie yoki donut kabi boshqa narsani tasavvur qilishingiz mumkin, lekin men to'pni tasavvur qilaman:
Agar biz bu qutini tortish maydonlari bo'lmagan yoki boshqa joyga ega bo'lmagan joyga olib boradigan bo'lsak, u holda to'pning holatiga ta'sir qilishi mumkin. Siz qutini har qanday kosmik jismlardan juda uzoqda bo'lgan kosmosda tasavvur qilishingiz mumkin, yoki bunday joyni topish qiyin bo'lsa, hech bo'lmaganda sayyora atrofida aylanadigan kosmik kemani tasavvur qiling, u erda hamma narsa vaznsiz holatda. Yuqoridagi rasmdan ko'rishingiz mumkinki, biz har bir o'qga bir juft devor belgilaymiz (biz qutining ichiga qarashimiz uchun Y+ devorini olib tashladik). Tasavvur qiling, har bir devor bosimga sezgir. Agar biz birdaniga qutini chapga siljitsak (1g = 9.8m/s^2 tezlashtirish bilan tezlashtiramiz), to'p X- devoriga tegadi. Keyin to'p devorga qo'llaniladigan bosim kuchini o'lchaymiz va X o'qida -1g qiymatini chiqaramiz.
E'tibor bering, akselerometr tezlashuv vektoridan qarama -qarshi yo'naltirilgan kuchni aniqlaydi. Bu kuch ko'pincha inertial kuch yoki xayoliy kuch deb ataladi. Siz bundan o'rganishingiz kerak bo'lgan narsa shundaki, akselerometr tezlikni bilvosita uning devorlaridan biriga ta'sir qiladigan kuch bilan o'lchaydi (bizning modelimizga ko'ra, bu haqiqiy hayot akselerometrlarida bahor yoki boshqa narsa bo'lishi mumkin). Bu kuch tezlashuvdan kelib chiqishi mumkin, lekin keyingi misolda ko'rib turganimizdek, bu har doim ham tezlashuvdan kelib chiqmaydi.
Agar biz o'z modelimizni olib, uni Yerga qo'ysak, to'p Z devoriga tushadi va pastki rasmda ko'rsatilgandek, pastki devorga 1 g kuch qo'llaniladi:
Bu holda quti qimirlamaydi, lekin biz hali ham Z o'qida -1g ko'rsatkichini olamiz. To'pning devorga bosilishi tortishish kuchi tufayli sodir bo'lgan. Nazariy jihatdan, bu boshqa turdagi kuch bo'lishi mumkin - masalan, agar siz bizning to'pimiz metall ekanligini tasavvur qilsangiz, magnitni qutining yoniga qo'yish, to'pni boshqa devorga urib yuborishi mumkin. Bu faqat akselerometr o'lchovlari tezlashuv emas, kuch berishini isbotlash uchun aytilgan. Bu tezlashuv akselerometrning kuchini aniqlash mexanizmi tomonidan qo'lga olinadigan inertial kuchga olib keladi.
Bu model MEMS sensori qanday tuzilganiga to'g'ri kelmasa ham, u tez -tez akselerometr bilan bog'liq muammolarni hal qilishda foydalidir. Haqiqatan ham shunga o'xshash sensorlar borki, ular ichida metall sharlar bor, ular burilish kalitlari deb ataladi, lekin ular ancha sodda va odatda ular faqat qurilmaning nishablik chegarasi emas, balki ma'lum bir chegaraga moyilligini aniqlay oladi.
Hozircha biz bitta o'qda akselerometrning chiqishini tahlil qildik va bu faqat bitta o'qli akselerometr bilan siz oladigan narsadir. Uch eksenli akselerometrlarning haqiqiy qiymati ular uchta o'qda ham inert kuchlarni aniqlay olishidan kelib chiqadi. Keling, quti modeliga qaytamiz va qutini 45 gradus o'ng tomonga buramiz. To'p 2 devorga tegadi: Z- va X- quyidagi rasmda ko'rsatilgandek:
0.71 qiymatlari o'zboshimchalik bilan emas, ular aslida SQRT (1/2) uchun taxminiydir. Bu akselerometrning keyingi modelini tanishtirganimizda aniqroq bo'ladi.
Oldingi modelda biz tortish kuchini aniqladik va xayoliy qutimizni aylantirdik. Oxirgi 2 ta misolda biz chiqishni 2 xil quti holatida tahlil qildik, kuch vektori esa o'zgarmadi. Bu akselerometrning tashqi kuchlar bilan o'zaro ta'sirini tushunishda foydali bo'lgan bo'lsa -da, agar biz koordinata tizimini akselerometr o'qlariga o'rnatib, kuch vektori bizni atrofida aylanayotganini tasavvur qilsak, hisob -kitoblarni amalga oshirish amaliyroq bo'ladi.
Iltimos, yuqoridagi modelni ko'rib chiqing, men o'qlarning ranglarini saqlab qoldim, shunda siz avvalgi modeldan yangisiga aqliy o'tishingiz mumkin. Tasavvur qiling -a, yangi modeldagi har bir o'q oldingi modeldagi qutining tegishli yuzlariga perpendikulyar. V vektor - bu akselerometr o'lchaydigan kuch vektori (bu tortishish kuchi yoki yuqoridagi misollardan inersial kuch yoki ikkalasining kombinatsiyasi bo'lishi mumkin). Rx, Ry, Rz - X vektorining X, Y, Z o'qlariga proektsiyasi. Iltimos, quyidagi munosabatlarga e'tibor bering:
R^2 = Rx^2 + Ry^2 + Rz^2 (1 -tenglama)
bu asosan 3D formatidagi Pifagor teoremasiga tengdir.
Esingizda bo'lsa, biroz oldin men sizga SQRT (1/2) ~ 0.71 qiymatlari tasodifiy emasligini aytgandim. Agar siz ularni yuqoridagi formulaga ulasangiz, bizning tortishish kuchi 1 g ekanligini eslaganimizdan so'ng, biz buni tasdiqlashimiz mumkin:
1^2 = (-SQRT (1/2))^2 + 0^2 + (-SQRT (1/2))^2
1 -tenglamada R = 1, Rx = -SQRT (1/2), Ry = 0, Rz = -SQRT (1/2) ni almashtirish orqali.
Uzoq nazariyadan so'ng biz haqiqiy hayot akselerometrlariga yaqinlashamiz. Rx, Ry, Rz qiymatlari aslida sizning real akselerometringiz chiqaradigan va har xil hisob-kitoblarni amalga oshirish uchun ishlatadigan qiymatlar bilan chiziqli bog'liqdir.
U erga borishdan oldin, akselerometrlarning bu ma'lumotni bizga qanday etkazishi haqida bir oz gaplashaylik. Akselerometrlarning aksariyati ikkita toifaga bo'linadi: raqamli va analog. Raqamli akselerometrlar sizga I2C, SPI yoki USART kabi ketma -ket protokoldan foydalangan holda ma'lumot beradi, analog akselerometrlar esa ADC (analogdan raqamli konvertor) moduli yordamida raqamli qiymatga o'tishingiz kerak bo'lgan oldindan belgilangan diapazonda kuchlanish darajasini chiqaradi. Men ADC qanday ishlashi haqida batafsil ma'lumot bermayman, qisman bu juda keng mavzu va qisman bir platformadan boshqasiga farq qiladi. Ba'zi mikrokontrolderlarda o'rnatilgan ADC modullari bo'ladi, ulardan ba'zilari ADC konvertatsiyasini amalga oshirish uchun tashqi komponentlarga muhtoj bo'ladi. Qaysi turdagi ADC modulidan qat'i nazar, siz ma'lum bir diapazonda qiymatga ega bo'lasiz. Masalan, 10 bitli ADC moduli 0..1023 oralig'ida qiymat chiqaradi, 1023 = 2^10 -1 ga e'tibor bering. 12 bitli ADC moduli 0..4095 oralig'ida qiymat chiqaradi, 4095 = 2^12-1 ga e'tibor bering.
Oddiy misolni ko'rib chiqaylik, 10bitli ADC moduli bizga uchta akselerometr kanali (o'qi) uchun quyidagi qiymatlarni berdi deylik:
AdcRx = 586 AdcRy = 630 AdcRz = 561
Har bir ADC moduli mos yozuvlar zo'riqishida bo'ladi, bizning misolimizda bu 3,3V. 10 bitlik ADC qiymatini kuchlanishga aylantirish uchun quyidagi formuladan foydalanamiz:
VoltsRx = AdcRx * Vref / 1023
Bu erda tezkor eslatma: 8 bitli ADC uchun oxirgi bo'luvchi 255 = 2 ^ 8 -1 bo'ladi va 12 bitli ADC uchun oxirgi bo'luvchi 4095 = 2 ^ 12 -1 bo'ladi.
Ushbu formulani barcha 3 kanalga qo'llagan holda biz olamiz:
VoltsRx = 586 * 3.3V / 1023 = ~ 1.89V (barcha natijalarni 2 kasrli nuqtaga yaxlitlaymiz) VoltsRy = 630 * 3.3V / 1023 = ~ 2.03V VoltsRz = 561 * 3.3V / 1023 = ~ 1.81V
Har bir akselerometr nol-g kuchlanish darajasiga ega, siz uni texnik xususiyatlardan topishingiz mumkin, bu kuchlanish 0g ga to'g'ri keladi. Imzolangan kuchlanish qiymatini olish uchun biz bu darajadan siljishni hisoblashimiz kerak. Aytaylik, bizning 0g kuchlanish darajasi VzeroG = 1.65V. Nol-g kuchlanishdan kuchlanish o'zgarishini quyidagicha hisoblaymiz:
DeltaVoltsRx = 1.89V - 1.65V = 0.24V DeltaVoltsRy = 2.03V - 1.65V = 0.38V DeltaVoltsRz = 1.81V - 1.65V = 0.16V
Bizda hozirda akselerometr ko'rsatkichlari Voltda, u hali g (9,8 m/s^2) da emas, oxirgi konvertatsiya qilish uchun biz odatda mV/g bilan ifodalangan akselerometr sezuvchanligini qo'llaymiz. Aytaylik, bizning sezgirligimiz = 478.5mV/g = 0.4785V/g. Sezuvchanlik qiymatlarini akselerometr spetsifikatsiyalarida topish mumkin. G bilan ifodalangan oxirgi kuch qiymatlarini olish uchun biz quyidagi formuladan foydalanamiz:
Rx = DeltaVoltsRx / sezuvchanlik
Rx = 0.24V / 0.4785V / g = ~ 0.5g Ry = 0.38V / 0.4785V / g = ~ 0.79g Rz = 0.16V / 0.4785V / g = ~ 0.33g
Biz, albatta, barcha qadamlarni bitta formulada birlashtira olamiz, lekin men ADC o'qishidan g bilan ifodalangan kuch vektorining komponentiga qanday o'tishingizni tushuntirish uchun barcha qadamlarni bosib o'tdim.
Rx = (AdcRx * Vref / 1023 - VzeroG) / sezuvchanlik (tenglama 2) Ry = (AdcRy * Vref / 1023 - VzeroG) / sezuvchanlik Rz = (AdcRz * Vref / 1023 - VzeroG) / sezuvchanlik
Hozirda bizda inertial kuch vektorini aniqlaydigan 3 ta komponent bor, agar qurilma tortishish kuchidan boshqa kuchlarga ta'sir qilmasa, bu bizning tortishish kuchi vektorining yo'nalishi deb taxmin qilishimiz mumkin. Agar siz qurilmaning erga nisbatan moyilligini hisoblamoqchi bo'lsangiz, bu vektor va Z o'qi orasidagi burchakni hisoblashingiz mumkin. Agar siz ham o'qning moyillik yo'nalishi bilan qiziqsangiz, bu natijani 2 komponentga bo'lishingiz mumkin: tortishish vektori va X / Y o'qlari orasidagi burchak sifatida hisoblanishi mumkin bo'lgan X va Y o'qidagi moyillik. Bu burchaklarni hisoblash siz o'ylagandan ko'ra sodda, endi biz Rx, Ry va Rz qiymatlarini hisoblab chiqdik. Keling, oxirgi akselerometr modeliga qaytamiz va qo'shimcha yozuvlarni bajaramiz:
Bizni qiziqtiradigan burchaklar X, Y, Z o'qlari va R vektor kuchlari orasidagi burchaklardir. Biz bu burchaklarni Axr, Ayr, Azr deb belgilaymiz. R va Rx tomonidan hosil qilingan to'g'ri burchakli uchburchakdan quyidagini sezishingiz mumkin:
cos (Axr) = Rx / R va shunga o'xshash: cos (Ayr) = Ry / R cos (Azr) = Rz / R
Biz 1 -tenglamadan R = SQRT (Rx^2 + Ry^2 + Rz^2) ni chiqarib olamiz.
Endi biz burchaklarni arccos () funktsiyasidan (teskari cos () funktsiyasi) foydalanib topishimiz mumkin:
Axr = arccos (Rx/R) Ayr = arccos (Ry/R) Azr = arccos (Rz/R)
Biz akselerometr modelini tushuntirish uchun uzoq yo'lni bosib o'tdik, faqat shu formulalarga kelishimiz kerak. Ilovalaringizga qarab, biz hosil qilgan har qanday oraliq formulalardan foydalanishni xohlashingiz mumkin. Biz ham tez orada giroskop modelini taqdim etamiz va moyillikni aniqroq baholash uchun akselerometr va giroskop ma'lumotlarini qanday birlashtirish mumkinligini ko'rib chiqamiz.
Ammo buni qilishdan oldin, keling, yana bir nechta foydali eslatmalarni bajaraylik:
cosX = cos (Axr) = Rx / R qulay = cos (Ayr) = Ry / R cosZ = cos (Azr) = Rz / R
Bu uchlik ko'pincha Yo'nalish kosinusi deb ataladi va u asosan bizning R vektorimiz bilan bir xil yo'nalishdagi birlik vektorini (uzunligi 1 bo'lgan vektor) ifodalaydi. Siz buni osongina tekshirishingiz mumkin:
SQRT (cosX^2 + qulay^2 + cosZ^2) = 1
Bu yaxshi xususiyat, chunki u bizni R vektorining modulini (uzunligini) kuzatishdan ozod qiladi. Ko'pincha bizni inertial vektorimiz yo'nalishi qiziqtirsa, boshqa hisoblarni soddalashtirish uchun uning modulini normallashtirish mantiqan to'g'ri keladi.
2 -qadam: giroskop
Biz akselerometrda bo'lgani kabi giroskop uchun ham xuddi shunday quti modelini kiritmaymiz, aksincha, biz ikkinchi akselerometr modeliga o'tamiz va biz bu modelga muvofiq giroskop nimani o'lchashini ko'rsatamiz.
Har bir giroskop kanali o'qlardan birining aylanishini o'lchaydi. Masalan, 2 o'qli giroskop X va Y o'qlarining aylanishini o'lchaydi (yoki ba'zilar "taxminan" deyishi mumkin). Bu aylanishni raqamlar bilan ifodalash uchun keling, bir nechta eslatmalarni bajaraylik. Avval aniqlaylik:
Rxz - bu inertial kuch vektorining R ning XZ tekisligidagi proyeksiyasi
Pxagor teoremasidan foydalanib, Rxz va Rz tomonidan yaratilgan to'g'ri burchakli uchburchakdan quyidagilarni olamiz:
Rxz^2 = Rx^2 + Rz^2 va shunga o'xshash: Ryz^2 = Ry^2 + Rz^2
shuningdek, e'tibor bering:
R^2 = Rxz^2 + Ry^2, bu tenglama 1 va yuqoridagi tenglamalardan yoki R va Ryz R^2 = Ryz^2 + Rx^2 hosil qilgan to'g'ri burchakli uchburchakdan olinishi mumkin.
Biz ushbu maqolada ushbu formulalarni ishlatmaymiz, lekin bizning modelimizdagi barcha qadriyatlar orasidagi bog'liqlikni qayd etish maqsadga muvofiqdir.
Buning o'rniga biz Z o'qi va Rxz, Ryz vektorlari orasidagi burchakni quyidagicha aniqlaymiz:
Axz - bu Rxz (R ning XZ tekisligidagi proyeksiyasi) va Z o'qining orasidagi ayz - Ryz (YZ tekisligidagi R proektsiyasi) va Z o'qi orasidagi burchak.
Endi biz giroskop o'lchagan narsalarga yaqinlashmoqdamiz. Gyroskop yuqorida ko'rsatilgan burchaklarning o'zgarish tezligini o'lchaydi. Boshqacha aytganda, bu burchaklarning o'zgarish tezligi bilan chiziqli bog'liq bo'lgan qiymatni chiqaradi. Buni tushuntirish uchun, biz t o'qisida Y o'qi (bu Axz burchagi bo'lardi) atrofida aylanish burchagini o'lchadik va uni Axz0 deb ta'riflaymiz, keyin bu burchakni t1 vaqtida o'lchadik va u Axz1 edi. O'zgarish tezligi quyidagicha hisoblanadi.
RateAxz = (Axz1 - Axz0) / (t1 - t0).
Agar biz Axzni darajalarda, vaqtni soniyalarda ifodalasak, bu qiymat deg/s bilan ifodalanadi. Bu giroskop o'lchagan narsadir.
Amalda, giroskop (agar u maxsus raqamli giroskop bo'lmasa) kamdan -kam hollarda deg/s bilan ifodalangan qiymatni beradi. Akselerometrda bo'lgani kabi, siz tenglamaga o'xshash formuladan foydalanib, deg/s ga aylantirishingiz kerak bo'lgan ADC qiymatini olasiz. 2 biz akselerometr uchun aniqladik. Keling, ADCni giroskop uchun deg/s konvertatsiya qilish formulasi bilan tanishtiraylik (biz 10 bitli ADC modulidan foydalanmoqdamiz, 8bitli ADC uchun 1023 ni 255 ga, 12bitli ADC uchun 1023ni 4095 bilan almashtiramiz).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivity Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Sezuvchanlik
AdcGyroXZ, AdcGyroYZ - bizning adc modulidan olingan va ular YZ tekisliklarida mos ravishda XZda R vektorining proyeksiyasini aylanishini o'lchaydigan kanallarni ifodalaydi, bu aylanishni mos ravishda Y va X o'qlari atrofida bajarishga tengdir.
Vref - biz VzeroRate pastidagi misolda biz 3,3V ishlatadigan ADC mos yozuvlar kuchlanishi - bu nol tezlikdagi kuchlanish, boshqacha aytganda, giroskop hech qanday aylanishga duch kelmaganida, Acc_Gyro platasi uchun masalan, 1,23V (siz bu qiymatlarni spetsifikatsiyalarda topishingiz mumkin) Sezuvchanlik - bu sizning giroskopingizning sezgirligi, mV / (deg / s) bilan ifodalanadi, ko'pincha mV / deg / s sifatida yoziladi, bu sizga asosan qancha mV bo'ladi agar siz aylanish tezligini bir deg/s ga oshirsangiz, giroskop chiqishi oshadi. Acc_Gyro platasining sezuvchanligi, masalan, 2mV/deg/s yoki 0,002V/deg/s
Misol keltiraylik, bizning ADC moduli quyidagi qiymatlarni qaytardi:
AdcGyroXZ = 571 AdcGyroXZ = 323
Yuqoridagi formuladan foydalangan holda va Acc_Gyro kartasining texnik parametrlaridan foydalanib, biz quyidagilarni olamiz:
RateAxz = (571 * 3.3V/1023 - 1.23V)/(0.002V/deg/s) = ~ 306 deg/s RateAyz = (323 * 3.3V/1023 - 1.23V)/(0.002V/deg/s) = ~ -94 daraja/s
Boshqacha qilib aytganda, qurilma Y o'qi atrofida (yoki XZ tekisligida aylanadi deb ayta olamiz) 306 gradus/s tezlikda va X o'qi atrofida aylanadi (yoki aytish mumkinki, YZ tekisligida aylanadi) - 94 daraja/s. E'tibor bering, salbiy belgi qurilmaning an'anaviy ijobiy yo'nalishdan teskari yo'nalishda aylanishini anglatadi. An'anaga ko'ra, aylanishning bitta yo'nalishi ijobiy. Yaxshi giroskop spetsifikatsiyasi varag'i sizga qaysi yo'nalish ijobiy ekanligini ko'rsatib beradi, aks holda siz uni qurilma bilan tajriba o'tkazib, chiqish pimidagi kuchlanishning oshishiga olib keladigan aylanishni aniqlab topishingiz kerak bo'ladi. Bu eng yaxshi osiloskop yordamida amalga oshiriladi, chunki siz aylanishni to'xtatishingiz bilan kuchlanish nol darajasiga tushadi. Agar siz multimetrdan foydalansangiz, siz kamida bir necha soniya davomida doimiy aylanish tezligini saqlab turishingiz va bu aylanish paytida kuchlanishni qayd etishingiz kerak, keyin uni nol tezlikdagi kuchlanish bilan solishtiring. Agar u nol darajali kuchlanishdan katta bo'lsa, bu aylanish yo'nalishi ijobiy ekanligini bildiradi.
3 -qadam: Accelerometer va Gyro -ni birlashtirish
Hammasini bir joyga to'plash - akselerometr va giroskop ma'lumotlarini birlashtirish
Agar siz ushbu maqolani o'qiyotgan bo'lsangiz, ehtimol siz IMU qurilmasini sotib olgansiz yoki sotib olmoqchisiz, yoki ehtimol siz alohida akselerometr va giroskop qurilmalaridan qurilmoqchisiz.
Akselerometr va giroskopni birlashtirgan IMU kombinatsiyalangan qurilmasidan foydalanishning birinchi qadami ularning koordinatali tizimlarini tekislashdir. Buning eng oson yo'li - akselerometrning koordinata tizimini mos yozuvlar koordinata tizimi sifatida tanlash. Akselerometr ma'lumotlarining ko'p varaqlari jismoniy chip yoki qurilma tasviriga nisbatan X, Y, Z o'qlarining yo'nalishini ko'rsatadi. Masalan, Acc_Gyro taxtasi spetsifikatsiyalarida ko'rsatilganidek, X, Y, Z o'qlarining yo'nalishlari:
Keyingi qadamlar:
RateAxz va RateAyz qiymatlariga mos keladigan giroskop chiqishlarini aniqlang, akselerometrga nisbatan giroskopning jismoniy joylashuvi tufayli bu chiqishlar teskari bo'lishi kerakligini aniqlang
Agar giroskopda X yoki Y belgili chiqish bo'lsa, u akselerometr koordinatalar tizimidagi har qanday o'qga to'g'ri keladi, deb o'ylamang, hatto bu chiqish IMU birligining bir qismi bo'lsa ham. Eng yaxshi usul - uni sinab ko'rish. Agar siz akselerometrga nisbatan giroskop o'rnini aniqlagan bo'lsangiz. Gyro va akselerometr chegaralari bir -biriga parallel, deb taxmin qilinadi, ya'ni siz gyrosni akselerometr chipiga nisbatan 90 daraja burchak ostida joylashtirasiz. Agar siz O'IH boshqaruv kengashini sotib olgan bo'lsangiz, ehtimol ular shu tarzda hizalanadi. Biz ushbu maqolada giroskop akselerometrga (masalan, 45 yoki 30 daraja) nisbatan noto'g'ri burchak ostida joylashtirilgan modellarni muhokama qilmaymiz, lekin bu ba'zi ilovalarda foydali bo'lishi mumkin.
Gyroskopning qaysi chiqishi yuqorida muhokama qilingan RateAxz qiymatiga mos kelishini aniqlash uchun namuna ketma -ketligi.
- qurilmani gorizontal holatda joylashtirishdan boshlang. Akselerometrning ikkala X va Y chiqishi nol-g kuchlanishni chiqaradi (masalan, Acc_Gyro platasi uchun bu 1,65V)
- keyingi navbatda qurilmani Y o'qi atrofida aylantirishni boshlang, boshqacha aytganda, siz qurilmani XZ tekisligida aylantirasiz, shunda X va Z akselerometrining chiqishlari o'zgaradi va Y chiqishi o'zgarmaydi. - gyroskop chiqishi o'zgaradigan qurilmani doimiy tezlikda aylantirganda, boshqa giroskop chiqishlari o'zgarmas bo'lishi kerak - Y o'qi atrofida aylanish paytida o'zgargan giroskop chiqishi (XZ tekisligida aylanish) AdcGyroXZ uchun kirish qiymatini beradi. biz RateAxzni hisoblaymiz - oxirgi qadam aylanish yo'nalishi bizning modelimizga mos kelishini ta'minlashdir, ba'zi hollarda akselerometrga nisbatan giroskopning jismoniy holati tufayli RateAxz qiymatini teskari o'zgartirishga to'g'ri keladi - yuqoridagi testni yana o'tkazing va qurilmani aylantiring. Y o'qi, bu safar akselerometrning X chiqishini kuzatadi (bizning modelimizda AdcRx). Agar AdcRx o'ssa (gorizontal holatidan birinchi 90 graduslik burilish), keyin AdcGyroXZ ham o'sishi kerak. Aks holda, siz RateAxz -ni teskari o'zgartirishingiz kerak bo'ladi, bunga quyidagicha tenglama 3 ga belgi faktorini kiritish orqali erishishingiz mumkin:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / sezuvchanlik, bu erda InvertAxz 1 yoki -1
Qurilmani X o'qi atrofida aylantirib, RateAyz uchun xuddi shunday sinov tayog'i o'tkaziladi va siz qaysi giroskop chiqishi RateAyzga mos kelishini va agar uni teskari aylantirish zarurligini aniqlasangiz bo'ladi. InvertAyz qiymatiga ega bo'lgach, RateAyzni hisoblash uchun quyidagi formuladan foydalanish kerak:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / sezuvchanlik
Agar siz ushbu testlarni Acc_Gyro doskasida o'tkazsangiz, siz quyidagi natijalarni olasiz:
- RateAxz uchun chiqish pimi GX4 va InvertAxz = -1. - RateAyz uchun chiqish pimi GY4 va InvertAyz = -1
Shu vaqtdan boshlab biz sizning IMU -ni Axr, Ayr, Azr (1 -qism. Akselerometr) va RateAxz, RateAyz (2 -bo'limda ko'rsatilganidek) to'g'ri qiymatlarini hisoblaydigan tarzda o'rnatgan deb hisoblaymiz.). Keyinchalik, biz ushbu qiymatlar orasidagi munosabatlarni tahlil qilamiz, ular qurilmaning er tekisligiga nisbatan moyilligini aniqroq baholashda foydali bo'ladi.
Siz o'zingizga savol berayotgandirsiz, agar akselerometr modeli bizga Axr, Ayr, Azr moyillik burchaklarini bergan bo'lsa, nega biz giroskop ma'lumotlari bilan bezovta qilmoqchimiz? Javob oddiy: akselerometr ma'lumotlariga har doim ham 100%ishonib bo'lmaydi. Shuni esda tutingki, akselerometr inertiya kuchini o'lchaydi, bunday kuch tortishish ta'sirida (va faqat idealda faqat tortishish kuchi bilan) paydo bo'lishi mumkin, lekin u qurilmaning tezlashishi (harakatlanishi) tufayli ham bo'lishi mumkin. Natijada, akselerometr nisbatan barqaror holatda bo'lsa ham, u umuman tebranish va mexanik shovqinlarga juda sezgir. Aksariyat IMU tizimlari akselerometr xatolarini yumshatish uchun giroskopdan foydalanishining asosiy sababi shu. Lekin bu qanday amalga oshiriladi? Va giroskop shovqinsizmi?
Gyroskop shovqindan xoli emas, lekin u aylanishni o'lchaganligi uchun chiziqli mexanik harakatlarga, akselerometr ta'sir qiladigan shovqin turiga nisbatan sezgir emas, lekin gyroskoplarda boshqa turdagi muammolar mavjud, masalan, drift (nol stavkasiga qaytmaydi) aylanish to'xtaganda). Shunga qaramay, akselerometr va giroskopdan olingan ma'lumotlarni o'rtacha hisoblab, biz faqat qurilma akselerometridan foydalanganimizdagidan ko'ra, hozirgi qurilmaning moyilligini yaxshiroq baholay olamiz.
Keyingi bosqichlarda men Kalman filtrida ishlatilgan ba'zi g'oyalardan ilhomlangan algoritmni joriy qilaman, lekin uni o'rnatilgan qurilmalarda qo'llash ancha sodda va osonroq. Avval biz algoritmimiz nimani hisoblashni xohlayotganini ko'rib chiqamiz. Xo'sh, bu tortishish kuchi vektorining yo'nalishi R = [Rx, Ry, Rz] biz undan Axr, Ayr, Azr yoki cosX, qulay, cosZ kabi boshqa qiymatlarni olishimiz mumkin, bu bizga qurilmamizning moyilligi haqida tasavvur beradi. er tekisligiga nisbatan, biz bu qiymatlar o'rtasidagi bog'liqlikni 1 -qismda muhokama qilamiz. Aytish mumkinki, bizda 1 -qismdagi 2 -tenglamadan Rx, Ry, Rz qiymatlari mavjud emasmi? Ha, lekin esda tutingki, bu qiymatlar faqat akselerometr ma'lumotlaridan olingan, shuning uchun agar siz ularni to'g'ridan -to'g'ri ilovangizda ishlatmoqchi bo'lsangiz, sizning dasturingiz toqat qilgandan ko'ra ko'proq shovqin olishingiz mumkin. Yana chalkashliklarga yo'l qo'ymaslik uchun, akselerometr o'lchovlarini quyidagicha qayta belgilaylik:
Racc - akselerometr bilan o'lchanadigan inertial kuch vektori, u quyidagi komponentlardan iborat (X, Y, Z o'qlari bo'yicha proektsiyalar):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Sezuvchanlik RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Sezuvchanlik RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Sezuvchanlik
Hozircha bizda ADC akselerometridan olishimiz mumkin bo'lgan o'lchovli qiymatlar to'plami mavjud. Biz bu ma'lumotlar to'plamini "vektor" deb ataymiz va biz quyidagi belgidan foydalanamiz.
Racc = [RxAcc, RyAcc, RzAcc]
Racc -ning bu komponentlarini akselerometr ma'lumotlaridan olish mumkin bo'lganligi sababli, biz uni algoritmimizga kirish deb hisoblashimiz mumkin.
E'tibor bering, Racc tortish kuchini o'lchaganligi uchun, agar siz ushbu vektorning uzunligi quyidagicha aniqlangan bo'lsa, siz to'g'ri bo'lamiz yoki 1g ga yaqin.
| Rakk | = SQRT (RxAcc^2 + RyAcc^2 + RzAcc^2), Biroq, bu vektorni quyidagicha yangilash mantiqiy:
Racc (normalizatsiya qilingan) = [RxAcc/| Racc |, RyAcc/| Racc |, RzAcc/| Racc |].
Bu sizning normalizatsiya qilingan Racc vektoringizning uzunligi har doim 1 bo'lishini ta'minlaydi.
Keyin biz yangi vektorni kiritamiz va uni chaqiramiz
Dam olish = [RxEst, RyEst, RzEst]
Bu bizning algoritmimiz natijasi bo'ladi, bu giroskop ma'lumotlariga asoslangan va o'tgan taxmin qilingan ma'lumotlarga asoslangan tuzatilgan qiymatlar.
Mana bizning algoritm nima qiladi: - akselerometr bizga: "Siz hozir Racc holatidasiz" - deymiz, "rahmat, lekin meni tekshirishga ruxsat bering" deymiz, - keyin bu ma'lumotni gyroskop ma'lumotlari bilan, shuningdek, o'tgan dam olish ma'lumotlari bilan to'g'rilang. biz "Rest" yangi taxminiy vektorini chiqaramiz. - biz "Rest" ni qurilmaning hozirgi holatiga nisbatan "eng yaxshi pul tikish" deb hisoblaymiz.
Keling, uni qanday ishlashini ko'rib chiqaylik.
Biz ketma -ketlikni akselerometrimizga ishonib va quyidagilarni belgilashdan boshlaymiz:
Dam olish (0) = Racc (0)
Aytgancha, Rest va Racc vektorlardir, shuning uchun yuqoridagi tenglama 3 ta tenglama yozishning oddiy usuli va takrorlanishdan saqlanish:
RxEst (0) = RxAcc (0) RyEst (0) = RyAcc (0) RzEst (0) = RzAcc (0)
Keyin biz T o'lchovlarining teng vaqt oralig'ida muntazam o'lchovlarni o'tkazamiz va biz Racc (1), Racc (2), Racc (3) va boshqalar kabi aniqlaydigan yangi o'lchovlarni olamiz. Shuningdek, biz dam olish (1), dam olish (2), dam olish (3) va hokazo vaqt oralig'ida yangi hisob -kitoblarni chiqaramiz.
Aytaylik, biz n -qadamdamiz. Biz foydalanmoqchi bo'lgan ikkita ma'lum qiymatlar to'plami bor:
Dam olish (n -1) - bizning oldingi bahoimiz, Rest (0) = Racc (0) Racc (n) bilan - bizning hozirgi akselerometr o'lchovimiz
Rest (n) ni hisoblashdan oldin, keling, gyroskopimizdan va oldingi bahodan olishimiz mumkin bo'lgan yangi o'lchangan qiymatni joriy qilaylik.
Biz uni Rgyro deb ataymiz va u ham 3 komponentdan iborat vektor:
Rgyro = [RxGyro, RyGyro, RzGyro]
Biz bu vektorni bir vaqtning o'zida bitta komponentni hisoblaymiz. Biz RxGyro -dan boshlaymiz.
Gyroskop modelimizda quyidagi munosabatni kuzatishdan boshlaylik, Rz va Rxz tomonidan hosil qilingan to'g'ri burchakli uchburchakdan quyidagini chiqarishimiz mumkin:
tan (Axz) = Rx/Rz => Axz = atan2 (Rx, Rz)
Atan2 siz ilgari ishlatmagan funksiya bo'lishi mumkin, lekin u atanga o'xshaydi, faqat atan tomonidan qaytarilgan (-PI/2, PI/2) dan farqli o'laroq (-PI, PI) oralig'idagi qiymatlarni qaytaradi va bu kerak Bitta argument o'rniga 2 ta argument. Bu bizga ikkita Rx, Rz qiymatlarini 360 graduslik burchaklarga aylantirish imkonini beradi (-PIdan PIgacha). Bu erda atan2 haqida ko'proq o'qishingiz mumkin.
Shunday qilib, RxEst (n-1) va RzEst (n-1) ni bilishimiz mumkin:
Axz (n-1) = atan2 (RxEst (n-1), RzEst (n-1)).
Esda tutingki, giroskop Axz burchagining o'zgarish tezligini o'lchaydi. Shunday qilib, biz Axz (n) yangi burchagini quyidagicha baholay olamiz:
Axz (n) = Axz (n-1) + RateAxz (n) * T
Esda tutingki, RateAxz -ni bizning ADC gyroskop o'qishlarimizdan olish mumkin. Aniqroq formulada o'rtacha aylanish tezligi quyidagicha hisoblanishi mumkin:
RateAxzAvg = (RateAxz (n) + RateAxz (n-1)) / 2 Axz (n) = Axz (n-1) + RateAxzAvg * T
Xuddi shu tarzda biz topa olamiz:
Ayz (n) = Ayz (n-1) + RateAyz (n) * T
Xo'sh, endi bizda Axz (n) va Ayz (n) bor. Bu erdan RxGyro/RyGyro -ni olib tashlash uchun qaerga boramiz? Ekvivalentdan 1 biz Rgyro vektorining uzunligini quyidagicha yozishimiz mumkin:
| Rgyro | = SQRT (RxGyro^2 + RyGyro^2 + RzGyro^2)
Bundan tashqari, biz Racc vektorini normal holatga keltirganimiz uchun, uning uzunligi 1 ga teng va u aylanishdan keyin o'zgarmagan deb taxmin qilishimiz mumkin, shuning uchun yozish nisbatan xavfsiz:
| Rgyro | = 1
Quyidagi hisob -kitoblar uchun vaqtinchalik qisqartirilgan yozuvni qabul qilaylik:
x = RxGyro, y = RyGyro, z = RzGyro
Yuqoridagi munosabatlardan foydalanib, biz quyidagilarni yozishimiz mumkin:
x = x / 1 = x / SQRT (x^2+y^2+z^2)
Hisoblagich va maxrajni SQRT (x^2 + z^2) ga ajratamiz.
x = (x / SQRT (x^2 + z^2)) / SQRT ((x^2 + y^2 + z^2) / (x^2 + z^2))
E'tibor bering, x / SQRT (x^2 + z^2) = sin (Axz), shuning uchun:
x = sin (Axz) / SQRT (1 + y^2 / (x^2 + z^2))
Endi SQRT ichidagi kasrning hisoblagichi va maxrajini z^2 ga ko'paytiring
x = sin (Axz) / SQRT (1 + y^2 * z^2 / (z^2 * (x^2 + z^2)))
E'tibor bering, z / SQRT (x^2 + z^2) = cos (Axz) va y / z = tan (Ayz), shuning uchun nihoyat:
x = sin (Axz) / SQRT (1 + cos (Axz)^2 * tan (Ayz)^2)
Belgilarimizga qaytsak, biz quyidagilarni olamiz:
RxGyro = sin (Axz (n)) / SQRT (1 + cos (Axz (n))^2 * tan (Ayz (n))^2)
biz ham xuddi shunday topamiz
RyGyro = sin (Ayz (n)) / SQRT (1 + cos (Ayz (n))^2 * tan (Axz (n))^2)
Endi, nihoyat, biz topa olamiz:
RzGyro = Belgi (RzGyro)*SQRT (1 - RxGyro^2 - RyGyro^2).
Bu erda RzGyro> = 0 bo'lganda Sign (RzGyro) = 1 va RzGyro <0 bo'lganda Sign (RzGyro) = -1.
Buni taxmin qilishning oddiy usullaridan biri:
Belgi (RzGyro) = Belgi (RzEst (n-1))
Amalda, RzEst (n-1) 0 ga yaqin bo'lganda ehtiyot bo'ling. Bunday holda siz gyro fazasini umuman o'tkazib yuborishingiz mumkin: Rgyro = Rest (n-1). Rz Axz va Ayz burchaklarini hisoblash uchun mos yozuvlar sifatida ishlatiladi va 0 ga yaqin bo'lsa, qiymatlar haddan tashqari oqishi va yomon natijalarga olib kelishi mumkin. Tan () / atan () funktsiyasini bajarishda aniqlik bo'lmasligi mumkin bo'lgan katta suzuvchi nuqta raqamlari domenida bo'lasiz.
Shunday qilib, biz hozirgacha mavjud bo'lgan narsalarni umumlashtiramiz, biz algoritmimizning n -bosqichidamiz va quyidagi qiymatlarni hisoblab chiqdik:
Racc - bizning Rgyro akselerometrimizdagi joriy ko'rsatkichlar - Rest (n -1) va hozirgi giroskop ko'rsatkichlaridan olingan.
Rest (n) yangilangan smetasini hisoblash uchun qaysi qiymatlardan foydalanamiz? Siz ikkalasini ham ishlatamiz deb taxmin qilgansiz. Biz o'rtacha vazndan foydalanamiz, shuning uchun:
Dam olish (n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
Biz bu formulani soddalashtirishimiz mumkin, bu ham kasrning sonini, ham maxrajini w1 ga bo'lish orqali.
Dam olish (n) = (Racc * w1/w1 + Rgyro * w2/w1)/(w1/w1 + w2/w1)
va w2/w1 = wGyro -ni almashtirgandan so'ng, biz olamiz:
Dam olish (n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
Yuqoridagi forumda wGyro akselerometrga qaraganda biz girosimizga qanchalik ishonishimizni aytadi. Bu qiymat eksperimental tarzda tanlanishi mumkin, odatda 5 dan 20 gacha bo'lgan qiymatlar yaxshi natijalarga olib keladi.
Bu algoritmning Kalman filtridan asosiy farqi shundaki, bu og'irlik nisbatan qattiq, Kalman filtrida esa akselerometr ko'rsatkichlarining o'lchagan shovqini asosida og'irliklar doimiy ravishda yangilanadi. Kalman filtri sizga "eng yaxshi" nazariy natijalarni berishga qaratilgan, bu algoritm sizga amaliy qo'llanishingiz uchun "etarlicha yaxshi" natijalarni berishi mumkin. Siz o'lchagan ba'zi shovqin omillariga qarab wGyro -ni sozlaydigan algoritmni amalga oshirishingiz mumkin, lekin ko'pchilik ilovalar uchun belgilangan qiymatlar yaxshi ishlaydi.
Yangilangan taxminiy qiymatlarni olishimizga bir qadam qoldi:
RxEst (n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst (n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst (n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Endi bu vektorni yana normallashtiraylik:
R = SQRT (RxEst (n)^2 + RyEst (n)^2 + RzEst (n)^2)
RxEst (n) = RxEst (n)/R RyEst (n) = RyEst (n)/R RzEst (n) = RzEst (n)/R
Va biz o'z davrimizni yana takrorlashga tayyormiz.
Bu qo'llanma dastlab starlino.com saytida paydo bo'lgan, men bir nechta engil tahrirlar qildim va ruxsat bilan qayta joylashtirdim. Rahmat Starlino!
Tavsiya:
Raspberry Pi - ADXL345 3 o'qli akselerometr Python qo'llanmasi: 4 qadam

Raspberry Pi-ADXL345 3 o'qli akselerometr Python qo'llanmasi: ADXL345-bu kichik, ingichka, ultra quvvatli, 3 o'qli akselerometr, yuqori aniqlikdagi (13 bitli) o'lchami ± 16 g gacha. Raqamli chiqish ma'lumotlari 16 bitli ikkita qo'shimcha sifatida formatlangan va I2 C raqamli interfeysi orqali kirish mumkin. O'lchovlar
Micro: akselerometr bilan bitli robotni boshqarish: 4 qadam
Micro: bit robotlarini akselerometr yordamida boshqarish: Ushbu maqolada biz TinkerGen kompaniyasining BitCar to'plamidan foydalanib, Micro: bitli robotni quramiz va uni boshqa Micro: bitli platadagi akselerometr yordamida boshqaramiz. STEM ta'limi uchun mo'ljallangan robot. O'rnatish oson, masalan
MPU 6050 Gyro, Arduino bilan akselerometr aloqasi (Atmega328p): 5 qadam
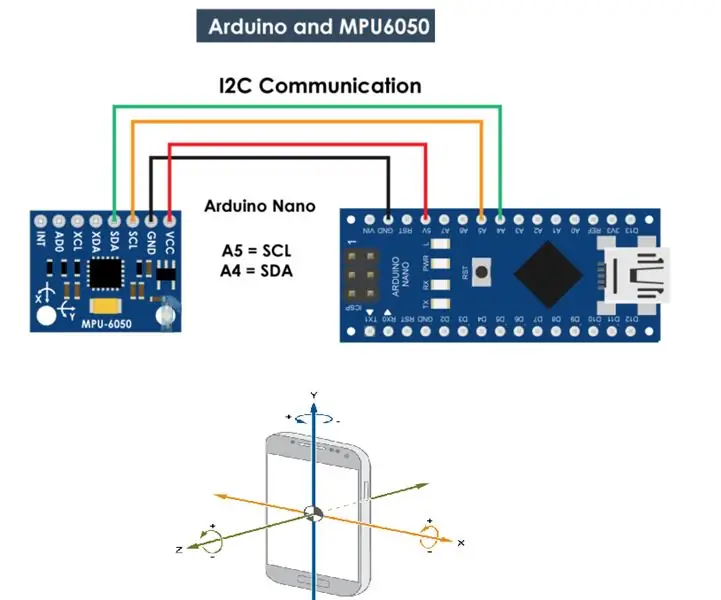
MPU 6050 Gyro, Arduino bilan akselerometr aloqasi (Atmega328p): MPU6050 IMU 3 o'qli akselerometr va bitta o'qga o'rnatilgan 3 o'qli giroskopga ega. X, Y va Z o'qlari. Gyroskopning natijalari
Raspberry Pi MMA8452Q 3 o'qli 12-bitli/8-bitli raqamli akselerometr Python qo'llanmasi: 4 qadam

Raspberry Pi MMA8452Q 3-o'qli 12-bitli/8-bitli raqamli akselerometr Python qo'llanmasi: MMA8452Q-bu 12 bitli aniqlikdagi aqlli, kam quvvatli, uch o'qli, sig'imli, mikromashinli akselerometr. Foydalanuvchilar tomonidan dasturlashtiriladigan moslashuvchan variantlar akselerometrga o'rnatilgan ikkita funktsiya yordamida ta'minlanadi, ular ikkita uzilishga o'rnatiladi
Gyro, akselerometr va Arduino yordamida burchakni o'lchash: 5 qadam

Gyro, akselerometr va Arduino yordamida burchakni o'lchash: qurilma - bu o'z -o'zidan muvozanatlanadigan robotning qo'pol prototipi, bu teshikning ikkinchi qismi (akselerometrni o'qing va dvigatelni o'z balansida boshqaring). Gyros bilan birinchi qismni bu erda topishingiz mumkin
